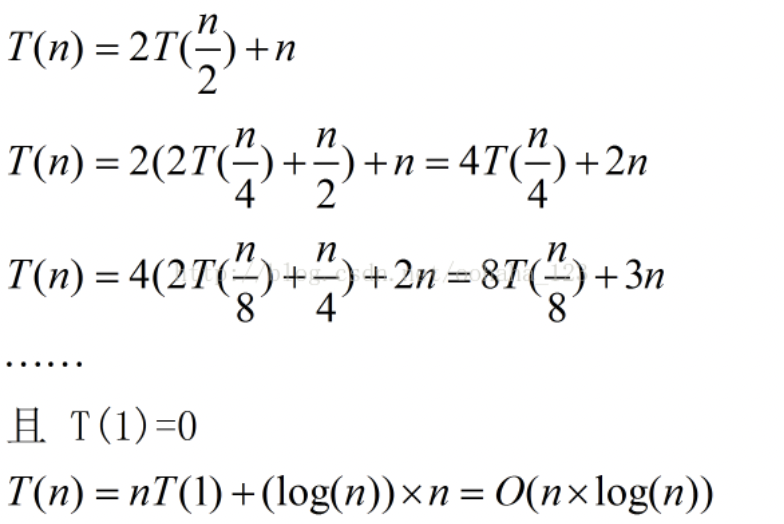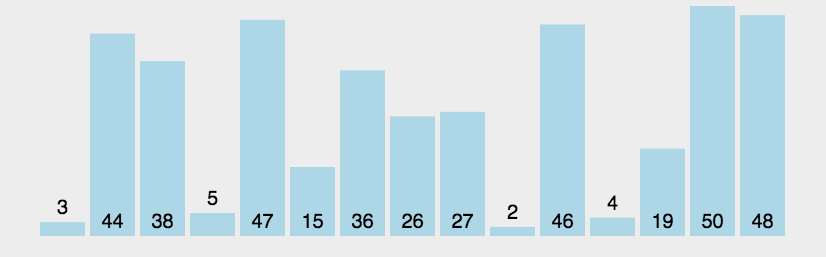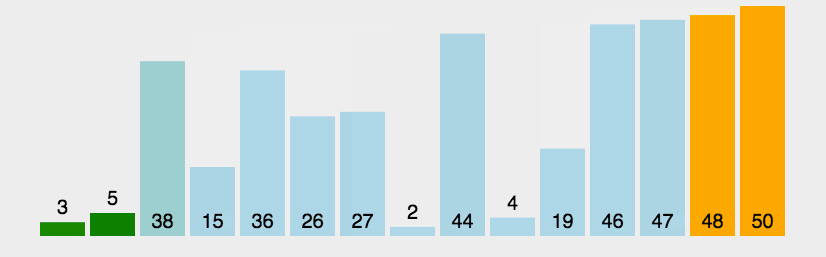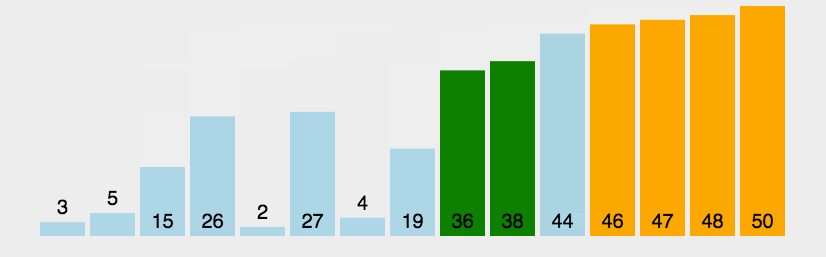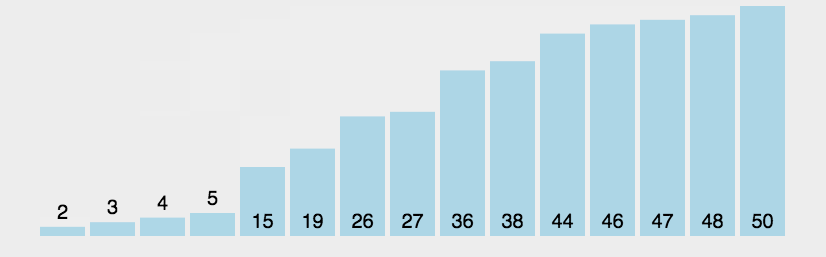面试官：说说你对归并排序的理解？如何实现？应用场景？

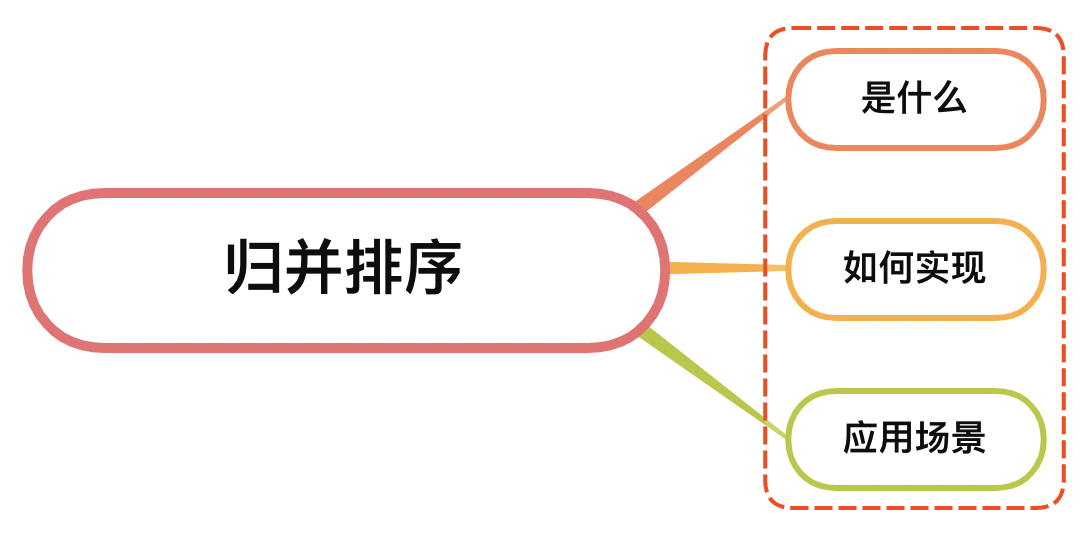
一、是什�?

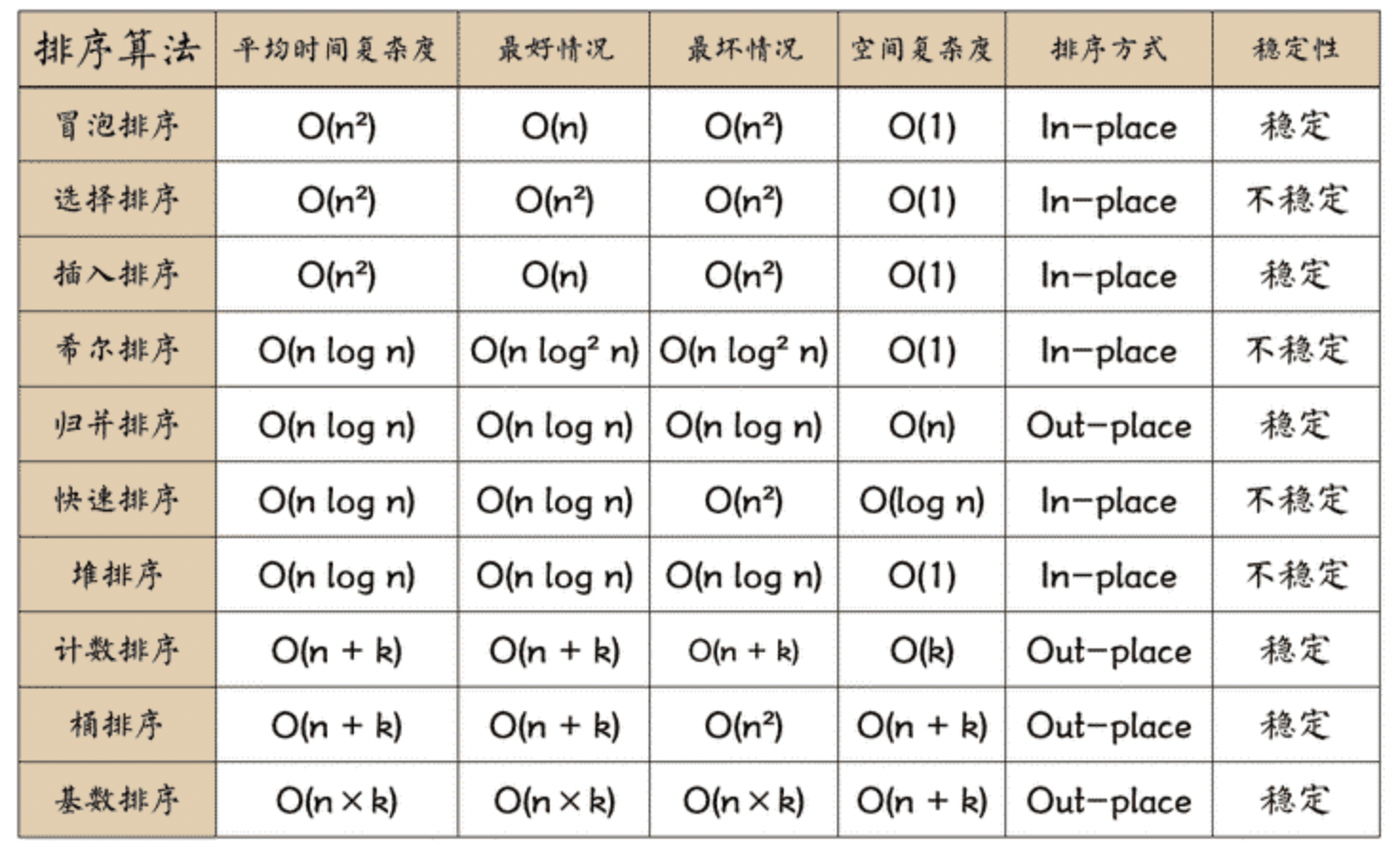
归并排序（Merge Sort）是建立归并操作上的一种有效，稳定的排序算法，该算法是采用分治法的一个非常典型的应用

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有�?
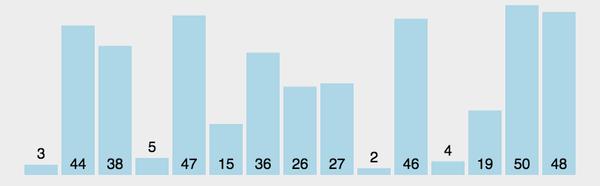
例如对于含有 n 个记录的无序表，首先默认表中每个记录各为一个有序表（只不过表的长度都为 1�?
然后进行两两合并，使 n 个有序表变为n/2 个长度为 2 或�?1 的有序表（例�?4 个小有序表合并为 2 个大的有序表�?
通过不断地进行两两合并，直到得到一个长度为 n 的有序表为止

例如对无序表{49�?8�?5�?7�?6�?3�?7}进行归并排序分成了分、合两部分：

如下图所示：

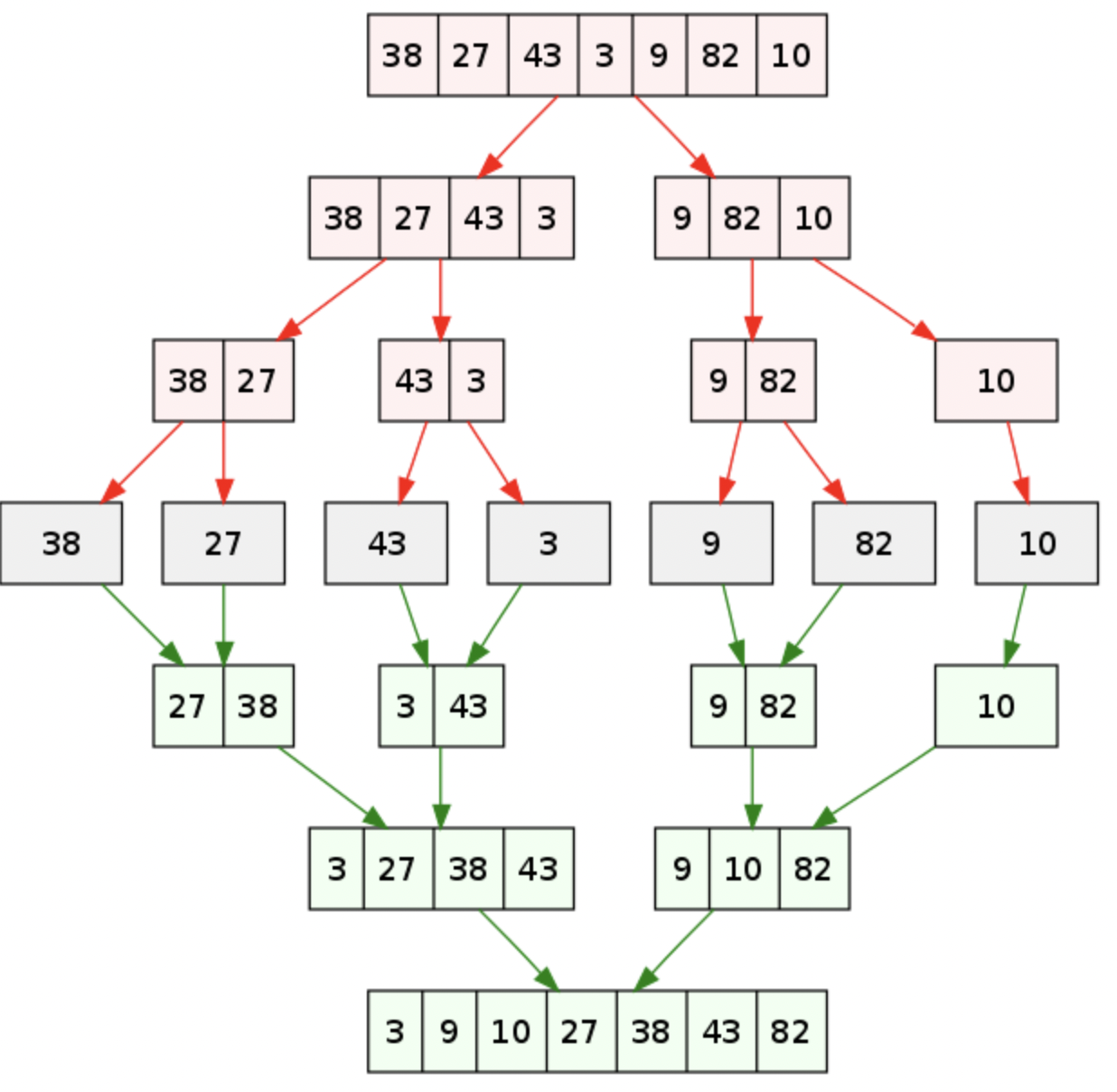
归并合过程中，每次得到的新的子表本身有序，所以最终得到有序表

上述分成两部分，则称为二路归并，如果分成三个部分则称为三路归并，以此类推

二、如何实�?

关于归并排序的算法思路如下�?

• 分：把数组分成两半，再递归对子数组进行分操作，直至到一个个单独数字

• 合：把两个数合成有序数组，再对有序数组进行合并操作，直到全部子数组合成一个完整的数组

  • 合并操作可以新建一个数组，用于存放排序后的数组
  • 比较两个有序数组的头部，较小者出队并且推入到上述新建的数组中
  • 如果两个数组还有值，则重复上述第二步
  • 如果只有一个数组有值，则将该数组的值出队并推入到上述新建的数组�?
    

用代码表示则如下图所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

function mergeSort(arr) {  // 采用自上而下的递归方法
    const len = arr.length;
    if(len < 2) {
        return arr;
    }
    let middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right)
{
    const result = [];

    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }

    while (left.length)
        result.push(left.shift());

    while (right.length)
        result.push(right.shift());

    return result;
}

上述归并分成了分、合两部分，在处理分过程中递归调用两个分的操作，所花费的时间为2乘T(n/2)，合的操作时间复杂度则为O(n)，因此可以得到以下公式：

总的执行时间 = 2 × 输入长度为n/2的sort函数的执行时�?+ merge函数的执行时间O(n)

当只有一个元素时，T(1) = O(1)

如果对T(n) = 2 * T(n/2) + O(n) 进行左右 / n的操作，得到 T(n) / n = (n / 2) * T(n/2) + O(1)

现在�?S(n) = T(n)/n，则S(1) = O(1)，然后利用表达式带入得到S(n) = S(n/2) + O(1)

所以可以得到：S(n) = S(n/2) + O(1) = S(n/4) + O(2) = S(n/8) + O(3) = S(n/2^k) + O(k) = S(1) + O(logn) = O(logn)

综上可得，T(n) = n * log(n) = nlogn

关于归并排序的稳定性，在进行合并过程，�?个或2个元素时�?个元素不会交换，2个元素如果大小相等也不会交换，由此可见归并排序是稳定的排序算�?

三、应用场�?

在外排序中通常使用排序-归并的策略，外排序是指处理超过内存限度的数据的排序算法，通常将中间结果放在读写较慢的外存储器，如下分成两个阶段：

• 排序阶段：读入能够放进内存中的数据量，将其排序输出到临时文件，一次进行，将带排序数据组织为多个有序的临时文件
• 归并阶段：将这些临时文件组合为大的有序文�?
  例如，使�?00m内存�?00m的数据进行排序，过程如下�?
• 读入100m数据内存，用常规方式排序
• 将排序后的数据写入磁�?- 重复前两个步骤，得到9�?00m的临时文�?- �?00m的内存划分为10份，�?份为输入缓冲区，�?0份为输出缓冲�?- 进行九路归并排序，将结果输出到缓冲区
  • 若输出缓冲区满，将数据写到目标文件，清空缓冲�? - 若缓冲区空，读入相应文件的下一份数�?

参考文�?

• https://baike.baidu.com/item/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F/1639015
• https://chowdera.com/2021/09/20210920201630258d.html#_127
• https://juejin.cn/post/6844904007899561998

面试官：说说你对快速排序的理解？如何实现？应用场景�?

一、是什�?

快速排序（Quick Sort）算法是在冒泡排序的基础上进行改进的一种算法，从名字上看就知道该排序算法的特点是快、效率高，是处理大数据最快的排序算法之一

实现的基本思想是：通过一次排序将整个无序表分成相互独立的两部分，其中一部分中的数据都比另一部分中包含的数据的值小

然后继续沿用此方法分别对两部分进行同样的操作，直到每一个小部分不可再分，所得到的整个序列就变成有序序列

例如，对无序�?9�?8�?5�?7�?6�?3�?7�?9进行快速排序，大致过程为：

• 首先从表中选取一个记录的关键字作为分割点（称为“枢轴”或者支点，一般选择第一个关键字），例如选取 49

• 将表格中大于 49 个放置于 49 的右侧，小于 49 的放置于 49 的左侧，假设完成后的无序表为：{27�?8�?3�?9�?5�?7�?6�?9}

• �?49 为支点，将整个无序表分割成了两个部分，分别为{27�?8�?3}和{65�?7�?6�?9}，继续采用此种方法分别对两个子表进行排序

• 前部分子表以 27 为支点，排序后的子表为{13�?7�?8}，此部分已经有序；后部分子表�?65 为支点，排序后的子表为{49�?5�?7�?6}

• 此时前半部分子表中的数据已完成排序；后部分子表继续以 65 为支点，将其分割为{49}和{97�?6}，前者不需排序，后者排序后的结果为{76�?97}

• 通过以上几步的排序，最后由子表{13�?7�?8}、{49}、{49}、{65}、{76�?7}构成有序表：{13�?7�?8�?9�?9�?5�?6�?7}

二、如何实�?

可以分成以下步骤�?

• 分区：从数组中选择任意一个基准，所有比基准小的元素放在基准的左边，比基准大的元素放到基准的右边
• 递归：递归地对基准前后的子数组进行分区

用代码表示则如下�?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function quickSort (arr) {
  const rec = (arr) => {
    if (arr.length <= 1) { return arr; }
    const left = [];
    const right = [];
    const mid = arr[0]; // 基准元素
    for (let i = 1; i < arr.length; i++){
      if (arr[i] < mid) {
        left.push(arr[i]);
      } else {
        right.push(arr[i]);
      }
    }
    return [...rec(left), mid, ...rec(right)]
  }
  return res(arr)
};

快速排序是冒泡排序的升级版，最坏情况下每一次基准元素都是数组中最小或者最大的元素，则快速排序就是冒泡排�?
这种情况时间复杂度就是冒泡排序的时间复杂度：T[n] = n * (n-1) = n^2 + n，也就是O(n^2)

最好情况下是O(nlogn)，其中递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n)，推导如下所示：

关于上述代码实现的快速排序，可以看到是稳定的

三、应用场�?

快速排序时间复杂度为O(nlogn)，是目前基于比较的内部排序中被认为最好的方法，当数据过大且数据杂乱无章时，则适合采用快速排�?

参考文�?

• https://baike.baidu.com/item/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95/369842
• https://www.cnblogs.com/l199616j/p/10597245.html

面试官：说说你对选择排序的理解？如何实现？应用场景？

一、是什�?

选择排序（Selection sort）是一种简单直观的排序算法，无论什么数据进去都�?O(n²) 的时间复杂度，所以用到它的时候，数据规模越小越好

其基本思想是：首先在未排序的数列中找到最�?or最�?元素，然后将其存放到数列的起始位�?
然后再从剩余未排序的元素中继续寻找最�?or最�?元素，然后放到已排序序列的末�?
以此类推，直到所有元素均排序完毕

举个例子，一个数组为 56�?2�?0�?1�?9，其排序过程如下�?

• 第一次遍历时，从下标�?1 的位置即 56 开始，找出关键字值最小的记录 12，同下标�?0 的关键字 56 交换位置。此时数组为 12�?6�?0�?1�?0

• 第二次遍历时，从下标�?2 的位置即 56 开始，找出最小�?20，同下标�?2 的关键字 56 互换位置，此时数组为12�?0�?0�?1�?6

• 第三次遍历时，从下标�?3 的位置即 80 开始，找出最小�?56，同下标�?3 的关键字 80 互换位置，此时数组为 12�?0�?6�?1�?0

• 第四次遍历时，从下标�?4 的位置即 91 开始，找出最小是 80，同下标�?4 的关键字 91 互换位置，此时排序完成，变成有序数组

二、如何实�?

从上面可以看到，对于具有 n 个记录的无序表遍�?n-1 次，第 i 次从无序表中�?i 个记录开始，找出后序关键字中最小的记录，然后放置在�?i 的位置上

直至到从第n个和第n-1个元素中选出最小的放在第n-1个位�?
如下动画所示：

用代码表示则如下�?

1
2
3
4
5
6
7
8
9
10
11
12
13
14

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的�?                minIndex = j;                 // 将最小数的索引保�?            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

第一次内循环比较N - 1次，然后是N-2次，N-3次，……，最后一次内循环比较1�?共比较的次数�?(N - 1) + (N - 2) + ... + 1，求等差数列和，�?(N - 1 + 1)* N / 2 = N^2 / 2，舍去最高项系数，其时间复杂度为 O(N^2)

从上述也可以看到，选择排序是一种稳定的排序

三、应用场�?

和冒泡排序一致，相比其它排序算法，这也是一个相对较高的时间复杂度，一般情况不推荐使用

但是我们还是要掌握冒泡排序的思想及实现，这对于我们的算法思维是有很大帮助�?

参考文�?

• https://baike.baidu.com/item/%E9%80%89%E6%8B%A9%E6%8E%92%E5%BA%8F/9762418
• https://zhuanlan.zhihu.com/p/29889599
• http://data.biancheng.net/view/72.html

面试官：说说你对集合的理解？常见的操作有哪些�?

一、是什�?

集合（Set），指具有某种特定性质的事物的总体，里面的每一项内容称作元�?
在数学中，我们经常会遇到集合的概念：

• 有限集合：例如一个班集所有的同学构成的集�?- 无限集合：例如全体自然数集合

在计算机中集合道理也基本一致，具有三大特性：

• 确定性：于一个给定的集合，集合中的元素是确定的。即一个元素，或者属于该集合，或者不属于该集合，两者必居其一
• 无序性：在一个集合中，不考虑元素之间的顺序，只要元素完全相同，就认为是同一个集�?- 互异性：集合中任意两个元素都是不同的

二、操�?

在ES6中，集合本身是一个构建函数Set，用来生�?Set 数据结构，如下：

1

const s = new Set();

关于集合常见的方法有�?

• add()：增
• delete()：删
• has()：改
• clear()：查

add()

添加某个值，返回 Set 结构本身

当添加实例中已经存在的元素，set不会进行处理添加

1
2
3
4
5
6
7
8
9

s.add(1).add(2).add(2); // 2只被添加了一�?```

体现了集合的互异性特�?
### delete()

删除某个值，返回一个布尔值，表示删除是否成功

```js
s.delete(1)

has()

返回一个布尔值，判断该值是否为Set的成�?

1

s.has(2)

clear()

清除所有成员，没有返回�?

1

s.clear()

关于多个集合常见的操作有�?

• 并集
• 交集
• 差集

并集

两个集合的共同元素，如下图所示：

代码实现方式如下�?

1
2
3
4
5
6

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// 并集
let union = new Set([...a, ...b]);
// Set {1, 2, 3, 4}

交集

两个集合A �?B，即属于A又属于B的元素，如下图所示：

用代码标识则如下�?

1
2
3
4
5
6

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// 交集
let intersect = new Set([...a].filter(x => b.has(x)));
// set {2, 3}

差集

两个集合A �?B，属于A的元素但不属于B的元素称为A相对于B的差集，如下图所示：

代码标识则如下：

1
2
3
4
5
6

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// （a 相对�?b 的）差集
let difference = new Set([...a].filter(x => !b.has(x)));
// Set {1}

三、应用场�?

一般情况下，使用数组的概率会比集合概率高很�?
使用set集合的场景一般是借助其确定性，其本身只包含不同的元�?
所以，可以利用Set的一些原生方法轻松的完成数组去重，查找数组公共元素及不同元素等操�?

参考文�?

• https://zh.wikipedia.org/wiki/%E5%B9%B6%E9%9B%86
• https://zh.wikipedia.org/wiki/%E8%A1%A5%E9%9B%86

面试官：说说常见的排序算法有哪些？区别？

一、是什�?

排序是程序开发中非常常见的操作，对一组任意的数据元素经过排序操作后，就可以把他们变成一组一定规则排序的有序序列

排序算法属于算法中的一种，而且是覆盖范围极小的一种，彻底掌握排序算法对程序开发是有很大的帮助�?
对与排序算法的好坏衡量，主要是从时间复杂度、空间复杂度、稳定�?
时间复杂度、空间复杂度前面已经讲过，这里主要看看稳定性的定义

稳定性指的是假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变

即在原序列中，r[i] = r[j]，且 r[i] �?r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的

二、有哪些

常见的算法排序算法有�?

• 冒泡排序
• 选择排序
• 插入排序
• 归并排序
• 快速排�?

冒泡排序

一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过�?
思路如下�?

• 比较相邻的元素，如果第一个比第二个大，就交换它们两个

• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的�?- 针对所有的元素重复以上的步骤，除了最后一�?- 重复上述步骤，直到没有任何一堆数字需要比�?
  

选择排序

选择排序是一种简单直观的排序算法，它也是一种交换排序算�?
无论什么数据进去都�?O(n²) 的时间复杂度。所以用到它的时候，数据规模越小越好

唯一的好处是不占用额外的内存存储空间

思路如下�?

• 在未排序序列中找到最小（大）元素，存放到排序序列的起始位�?- 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾�?- 重复第二步，直到所有元素均排序完毕

插入排序

插入排序是一种简单直观的排序算法

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

解决思路如下�?

• 把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序�?- 从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
• 重复上述过程直到最后一个元素被插入有序子数组中

归并排序

归并排序是建立在归并操作上的一种有效的排序算法

该算法是采用分治法的一个非常典型的应用

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有�?
解决思路如下�?

• 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
• 设定两个指针，最初位置分别为两个已经排序序列的起始位�?- 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
• 重复步骤3直到某一指针到达序列�?- 将另一序列剩下的所有元素直接复制到合并序列�?
  

快速排�?

快速排序是对冒泡排序算法的一种改进，基本思想是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要�?
再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列

解决思路如下�?

• 从数列中挑出一个元素，称为”基准”（pivot�?- 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操�?- 递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排�?
  

三、区�?

除了上述的排序算法之外，还存在其他的排序算法，例如希尔排序、堆排序等等……

区别如下图所示：

参考文�?

• https://www.runoob.com/w3cnote/bubble-sort.html
• http://www.x-lab.info/post/sort-algorithm/
• https://zhuanlan.zhihu.com/p/42586566

面试官：说说你对栈、队列的理解？应用场景？

一、栈

栈（stack）又名堆栈，它是一种运算受限的线性表，限定仅在表尾进行插入和删除操作的线性表

表尾这一端被称为栈顶，相反地另一端被称为栈底，向栈顶插入元素被称为进栈、入栈、压栈，从栈顶删除元素又称作出栈

所以其按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据，具有记忆作用

关于栈的简单实现，如下�?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Stack {
  constructor() {
    this.items = [];
  }

  /**
   * 添加一个（或几个）新元素到栈顶
   * @param {*} element 新元�?   */
  push(element) {
    this.items.push(element)
  }

  /**
   * 移除栈顶的元素，同时返回被移除的元素
   */
  pop() {
    return this.items.pop()
  }

  /**
   * 返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它�?   */
  peek() {
    return this.items[this.items.length - 1]
  }

  /**
   * 如果栈里没有任何元素就返回true,否则返回false
   */
  isEmpty() {
    return this.items.length === 0
  }

  /**
   * 移除栈里的所有元�?   */
  clear() {
    this.items = []
  }

  /**
   * 返回栈里的元素个数。这个方法和数组的length属性很类似
   */
  size() {
    return this.items.length
  }
}

关于栈的操作主要的方法如下：

• push：入栈操�?- pop：出栈操�?

二、队�?

跟栈十分相似，队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操�?
进行插入操作的端称为队尾，进行删除操作的端称为队头，当队列中没有元素时，称为空队�?
在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出

简单实现一个队列的方式，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Queue {
    constructor() {
        this.list = []
        this.frontIndex = 0
        this.tailIndex = 0
    }
    enqueue(item) {
        this.list[this.tailIndex++] = item
    }
    unqueue() {
        const item  = this.list[this.frontIndex]
        this.frontIndex++        
        return item
    }
}

上述这种入队和出队操作中，头尾指针只增加不减小，致使被删元素的空间永远无法重新利�?
当队列中实际的元素个数远远小于向量空间的规模时，也可能由于尾指针已超越向量空间的上界而不能做入队操作，出该现象称�?假溢”

在实际使用队列时，为了使队列空间能重复使用，往往对队列的使用方法稍加改进�?
无论插入或删除，一旦rear指针�?或front指针�? 时超出了所分配的队列空间，就让它指向这片连续空间的起始位置，这种队列也就是循环队列

下面实现一个循环队列，如下�?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Queue {
    constructor(size) {
        this.size = size; // 长度需要限�? 来达到空间的利用, 代表空间的长�?        this.list = [];
        this.font = 0; // 指向首元�?        this.rear = 0;  // 指向准备插入元素的位�?    }
    enQueue() {
        if (this.isFull() == true) {
            return false
        }
        this.rear = this.rear % this.k;
        this._data[this.rear++] = value;
        return true
    }
    deQueue() {
        if(this.isEmpty()){
            return false;
        }
        this.font++;
        this.font = this.font % this.k;
        return true;
    }
    isEmpty() {
        return this.font == this.rear - 1;
    }
    isFull() {
        return this.rear % this.k == this.font;
    }
}

上述通过求余的形式代表首尾指针增1 时超出了所分配的队列空�?

三、应用场�?

�?

借助栈的先进后出的特性，可以简单实现一个逆序数处的功能，首先把所有元素依次入栈，然后把所有元素出栈并输出

包括编译器的在对输入的语法进行分析的时候，例如"()"、"{}"、"[]"这些成对出现的符号，借助栈的特性，凡是遇到括号的前半部分，即把这个元素入栈，凡是遇到括号的后半部分就比对栈顶元素是否该元素相匹配，如果匹配，则前半部分出栈，否则就是匹配出�?
包括函数调用和递归的时候，每调用一个函数，底层都会进行入栈操作，出栈则返回函数的返回�?
生活中的例子，可以把乒乓球盒比喻成一个堆栈，球一个一个放进去（入栈），最先放进去的要等其后面的全部拿出来后才能出来（出栈），这种就是典型的先进后出模�?

队列

当我们需要按照一定的顺序来处理数据，而该数据的数据量在不断地变化的时候，则需要队列来帮助解题

队列的使用广泛应用在广度优先搜索种，例如层次遍历一个二叉树的节点值（后续将到�?
生活中的例子，排队买票，排在队头的永远先处理，后面的必须等到前面的全部处理完毕再进行处理，这也是典型的先进先出模�?

参考文�?

• https://baike.baidu.com/item/%E6%A0%88/12808149
• https://baike.baidu.com/item/%E9%98%9F%E5%88%97/14580481

面试官：说说你对数据结构的理解？有哪些？区别�?

一、是什�?

数据结构是计算机存储、组织数据的方式，是指相互之间存在一种或多种特定关系的数据元素的集合

前面讲到，一个程�?= 算法 + 数据结构，数据结构是实现算法的基础，选择合适的数据结构可以带来更高的运行或者存储效�?
数据元素相互之间的关系称为结构，根据数据元素之间关系的不同特性，通常有如下四类基本的结构�?

• 集合结构：该结构的数据元素间的关系是“属于同一个集合�?- 线性结构：该结构的数据元素之间存在着一对一的关�?- 树型结构：该结构的数据元素之间存在着一对多的关�?- 图形结构：该结构的数据元素之间存在着多对多的关系，也称网状结�?
  由于数据结构种类太多，逻辑结构可以再分成为�?
• 线性结构：有序数据元素的集合，其中数据元素之间的关系是一对一的关系，除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接�?- 非线性结构：各个数据元素不再保持在一个线性序列中，每个数据元素可能与零个或者多个其他数据元素发生关�?
  

二、有哪些

常见的数据结构有如下�?

• 数组
• �?- 队列
• 链表
• �?- �?- �?- 散列�?

数组

在程序设计中，为了处理方便， 一般情况把具有相同类型的若干变量按有序的形式组织起来，这些按序排列的同类数据元素的集合称为数组

�?

一种特殊的线性表，只能在某一端插入和删除的特殊线性表，按照先进后出的特性存储数�?
先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数�?

队列

跟栈基本一致，也是一种特殊的线性表，其特性是先进先出，只允许在表的前端进行删除操作，而在表的后端进行插入操作

链表

是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现�?
链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生�?
一般情况，每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域

�?

树是典型的非线性结构，在树的结构中，有且仅有一个根结点，该结点没有前驱结点。在树结构中的其他结点都有且仅有一个前驱结点，而且可以有两个以上的后继结点

�?

一种非线性结构。在图结结构中，数据结点一般称为顶点，而边是顶点的有序偶对。如果两个顶点之间存在一条边，那么就表示这两个顶点具有相邻关�?

�?

堆是一种特殊的树形数据结构，每个结点都有一个值，特点是根结点的值最小（或最大），且根结点的两个子树也是一个堆

散列�?

若结构中存在关键字和K相等的记录，则必定在f(K)的存储位置上，不需比较便可直接取得所查记�?

三、区�?

上述的数据结构，之前的区别可以分成线性结构和非线性结构：

• 线性结构有：数组、栈、队列、链表等
• 非线性结构有：树、图、堆�?

参考文�?

• https://zh.wikipedia.org/wiki/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84
• https://baike.baidu.com/item/数据结构/1450

面试官：说说你对算法中时间复杂度，空间复杂度的理解？如何计算�?

一、前言

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，但在过程中消耗的资源和时间却会有很大的区�?
衡量不同算法之间的优劣主要是通过时间�?*空间**两个维度去考量�?

• 时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述�?- 空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述

通常会遇到一种情况，时间和空间维度不能够兼顾，需要在两者之间取得一个平衡点是我们需要考虑�?
一个算法通常存在最好、平均、最坏三种情况，我们一般关注的是最坏情�?
最坏情况是算法运行时间的上界，对于某些算法来说，最坏情况出现的比较频繁，也意味着平均情况和最坏情况一样差

二、时间复杂度

时间复杂度是指执行这个算法所需要的计算工作量，其复杂度反映了程序执行时间「随输入规模增长而增长的量级」，在很大程度上能很好地反映出算法的优劣与否

一个算法花费的时间与算法中语句的「执行次数成正比」，执行次数越多，花费的时间就越�?
算法的复杂度通常用大O符号表述，定义为T(n) = O(f(n))，常见的时间复杂度有：O(1)常数型、O(log n)对数型、O(n)线性型、O(nlogn)线性对数型、O(n^2)平方型、O(n^3)立方型、O(n^k)k次方型、O(2^n)指数型，如下图所示：

从上述可以看到，随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低，由小到大排序如下�?

1

Ο(1)＜�?log n)＜�?n)＜�?nlog n)＜�?n2)＜�?n3)＜…＜Ο(2^n)＜�?n!)

注意的是，算法复杂度只是描述算法的增长趋势，并不能说一个算法一定比另外一个算法高效，如果常数项过大的时候也会导致算法的执行时间变长

关于如何计算时间复杂度，可以看看如下简单例子：

1
2
3
4
5
6
7
8
9

function process(n) {
  let a = 1
  let b = 2
  let sum = a + b
  for(let i = 0; i < n; i++) {
    sum += i
  }
  return sum
}

该函数算法需要执行的运算次数用输入大小n的函数表示，�?T(n) = 2 + n + 1，那么时间复杂度为O(n + 3)，又因为时间复杂度只关注最高数量级，且与之系数也没有关系，因此上述的时间复杂度为O(n)

又比如下面的例子�?

1
2
3
4
5
6
7
8

function process(n) {
 let count = 0
  for(let i = 0; i < n; i++){
    for(let i = 0; i < n; i++){
      count += 1
    }
  }
}

循环里面嵌套循环，外面的循环执行一次，里面的循环执行n次，因此时间复杂度为 O(n*n*1 + 2) = O(n^2)

对于顺序执行的语句，总的时间复杂度等于其中最大的时间复杂度，如下�?

1
2
3
4
5
6
7
8
9
10
11
12

function process(n) {
  let sum = 0
  for(let i = 0; i < n; i++) {
    sum += i
  }
  for(let i = 0; i < n; i++){
    for(let i = 0; i < n; i++){
      sum += 1
    }
  }
  return sum
}

上述第一部分复杂度为O(n)，第二部分复杂度为O(n^2)，总复杂度为max(O(n^2), O(n)) = O(n^2)

又如下一个例子：

1
2
3
4

function process(n) {
  let i = 1; // �?  while (i <= n) {
     i = i * 2; // �?  }
}

循环语句中以2的倍数来逼近n，每次都乘以2。如果用公式表示就是1 * 2 * 2 * 2 �?* 2 <=n，也就是�?的x次方小于等于n时会执行循环体，记作2^x <= n，于是得出x<=logn

因此循环在执行logn次之后，便结束，因此时间复杂度为O(logn)

同理，如果一个O(n)循环里面嵌套O(logn)的循环，则时间复杂度为O(nlogn)，像O(n^3)无非也就是嵌套了三层O(n)循环

三、空间复杂度

空间复杂度主要指执行算法所需内存的大小，用于对程序运行过程中所需要的临时存储空间的度�?
除了需要存储空间、指令、常数、变量和输入数据外，还包括对数据进行操作的工作单元和存储计算所需信息的辅助空�?
下面给出空间复杂度为O(1)的示例，如下

1
2
3

let a = 1
let b = 2
let c = 3

上述代码的临时空间不会随着n的变化而变化，因此空间复杂度为O(1)

1
2
3
4

let arr []
for(i=1; i<=n; ++i){
  arr.push(i)
}

上述可以看到，随着n的增加，数组的占用的内存空间越大

通常来说，只要算法不涉及到动态分配的空间，以及递归、栈所需的空间，空间复杂度通常为O(1)，一个一维数组a[n]，空间复杂度O(n)，二维数组为O(n^2)

参考文�?

• https://juejin.cn/post/6844904167824162823#heading-7

• https://zhuanlan.zhihu.com/p/50479555

• https://cloud.tencent.com/developer/article/1769988

面试官：说说你对树的理解？相关的操作有哪些？

一、是什�?

在计算机领域，树形数据结构是一类重要的非线性数据结构，可以表示数据之间一对多的关系。以树与二叉树最为常用，直观看来，树是以分支关系定义的层次结�?
二叉树满足以下两个条件：

• 本身是有序树
• 树中包含的各个结点的不能超过 2，即只能�?0�? 或�?2

如下图，左侧的为二叉树，而右侧的因为头结点的子结点超�?，因此不属于二叉树：

同时，二叉树可以继续进行分类，分成了满二叉树和完成二叉树�?

• 满二叉树：如果二叉树中除了叶子结点，每个结点的度都为 2

• 完成二叉树：如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布

二、操�?

关于二叉树的遍历，常见的有：

• 前序遍历

• 中序遍历

• 后序遍历

• 层序遍历

前序遍历

前序遍历的实现思想是：

• 访问根节�?- 访问当前节点的左子树
• 若当前节点无左子树，则访问当前节点的右子

根据遍历特性，递归版本用代码表示则如下�?

1
2
3
4
5
6

const preOrder = (root) => {
  if(!root){ return }
  console.log(root)
  preOrder(root.left)
  preOrder(root.right)
}

如果不使用递归版本，可以借助栈先进后出的特性实现，先将根节点压入栈，再分别压入右节点和左节点，直到栈中没有元素，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

const preOrder = (root) => {
  if(!root){ return }
  const stack = [root]
  while (stack.length) {
    const n = stack.pop()
    console.log(n.val)
    if (n.right) {
      stack.push(n.right)
    }
    if (n.left) {
      stack.push(n.left)
    }
  }
}

中序遍历

前序遍历的实现思想是：

• 访问当前节点的左子树
• 访问根节�?- 访问当前节点的右�?
  递归版本很好理解，用代码表示则如下：

1
2
3
4
5
6

const inOrder = (root) => {
  if (!root) { return }
  inOrder(root.left)
  console.log(root.val)
  inOrder(root.right)
}

非递归版本也是借助栈先进后出的特性，可以一直首先一直压入节点的左元素，当左节点没有后，才开始进行出栈操作，压入右节点，然后有依次压入左节点，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

const inOrder = (root) => {
  if (!root) { return }
  const stack = [root]
  let p = root
  while(stack.length || p){
    while (p) {
      stack.push(p)
      p = p.left
    }
    const n = stack.pop()
    console.log(n.val)
    p = n.right
  }
}

后序遍历

前序遍历的实现思想是：

• 访问当前节点的左子树
• 访问当前节点的右�?- 访问根节�?
  递归版本，用代码表示则如下：

1
2
3
4
5
6

const postOrder = (root) => {
  if (!root) { return }
  postOrder(root.left)
  postOrder(root.right)
  console.log(n.val)
 }

后序遍历非递归版本实际根全序遍历是逆序关系，可以再多创建一个栈用来进行输出，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

const preOrder = (root) => {
  if(!root){ return }
  const stack = [root]
  const outPut = []
  while (stack.length) {
    const n = stack.pop()
    outPut.push(n.val)
    if (n.right) {
      stack.push(n.right)
    }
    if (n.left) {
      stack.push(n.left)
    }
  }
  while (outPut.length) {
    const n = outPut.pop()
    console.log(n.val)
  }
}

层序遍历

按照二叉树中的层次从左到右依次遍历每层中的结�?
借助队列先进先出的特性，从树的根结点开始，依次将其左孩子和右孩子入队。而后每次队列中一个结点出队，都将其左孩子和右孩子入队，直到树中所有结点都出队，出队结点的先后顺序就是层次遍历的最终结�?
用代码表示则如下�?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

const levelOrder = (root) => {
    if (!root) { return [] }
    const queue = [[root, 0]]
    const res = []
    while (queue.length) {
        const n = queue.shift()
        const [node, leval] = n
        if (!res[leval]) {
            res[leval] = [node.val]
        } else {
            res[leval].push(node.val)
        }
        if (node.left) { queue.push([node.left, leval + 1]) }
        if (node.right) { queue.push([node.right, leval + 1]) }
    }
    return res
};

三、总结

树是一个非常重要的非线性结构，其中二叉树以二叉树最常见，二叉树的遍历方式可以分成前序遍历、中序遍历、后序遍�?
同时，二叉树又分成了完成二叉树和满二叉树

参考文�?

• https://baike.baidu.com/item/%E4%BA%8C%E5%8F%89%E6%A0%91
• http://data.biancheng.net/view/27.html

• 面试官：说说微信小程序的实现原理�?

  

一、背�?

网页开发，渲染线程和脚本是互斥的，这也是为什么长时间的脚本运行可能会导致页面失去响应的原因，本质就是我们常说�?JS 是单线程�?
而在小程序中，选择�?Hybrid 的渲染方式，将视图层和逻辑层是分开的，双线程同时运行，视图层的界面使用 WebView 进行渲染，逻辑层运行在 JSCore �?

• 渲染层：界面渲染相关的任务全都在 WebView 线程里执行。一个小程序存在多个界面，所以渲染层存在多个 WebView 线程
• 逻辑层：采用 JsCore 线程运行 JS 脚本，在这个环境下执行的都是有关小程序业务逻辑的代�?

二、通信

小程序在渲染层，宿主环境会把wxml转化成对应的JS对象

在逻辑层发生数据变更的时候，通过宿主环境提供的setData方法把数据从逻辑层传递到渲染层，再经过对比前后差异，把差异应用在原来的Dom树上，渲染出正确的视�?

当视图存在交互的时候，例如用户点击你界面上某个按钮，这类反馈应该通知给开发者的逻辑层，需要将对应的处理状态呈现给用户

对于事件的分发处理，微信进行了特殊的处理，将所有的事件拦截后，丢到逻辑层交给JavaScript进行处理

由于小程序是基于双线程的，也就是任何在视图层和逻辑层之间的数据传递都是线程间的通信，会有一定的延时，因此在小程序中，页面更新成了异步操�?
异步会使得各部分的运行时序变得复杂一些，比如在渲染首屏的时候，逻辑层与渲染层会同时开始初始化工作，但是渲染层需要有逻辑层的数据才能把界面渲染出�?
如果渲染层初始化工作较快完成，就要等逻辑层的指令才能进行下一步工�?
因此逻辑层与渲染层需要有一定的机制保证时序正确，在每个小程序页面的生命周期中，存在着若干次页面数据通信

三、运行机�?

小程序启动运行两种情况：

• 冷启动（重新开始）：用户首次打开或者小程序被微信主动销毁后再次打开的情况，此时小程序需要重新加载启动，即为冷启�? - 热启动：用户已经打开过小程序，然后在一定时间内再次打开该小程序，此时无需重新启动，只需要将后台态的小程序切换到前台，这个过程就是热启动

需要注意：

1.小程序没有重启的概念
2.当小程序进入后台，客户端会维持一段时间的运行状态，超过一定时间后会被微信主动销�?
3.短时间内收到系统两次以上内存警告，也会对小程序进行销毁，这也就为什么一旦页面内存溢出，页面会奔溃的本质原因�?

开发者在后台发布新版本之后，无法立刻影响到所有现网用户，但最差情况下，也在发布之�?24 小时之内下发新版本信息到用户

每次冷启动时，都会检查是否有更新版本，如果发现有新版本，将会异步下载新版本的代码包，并同时用客户端本地的包进行启动，即新版本的小程序需要等下一次冷启动才会应用�?

参考文�?

• https://developers.weixin.qq.com/community/develop/article/doc/0008a4c4f28f30fe3eb863b2750813
• https://juejin.cn/post/6976805521407868958#heading-5
• https://juejin.cn/post/6844903805675388942
• https://juejin.cn/post/6844903999863259144#heading-1